Henri Poincaré Father of Topology

date of birth : 29 April 1854                        

date of death : 17 July 1912                    

Nationality  : French                                                          

Institutions : Corps des Mines                      

                        Caen University

                        La Sorbonne

                        Bureau des Longitudes

Poincaré was clumsy and frail and supposedly flunked an IQ test, but he was one of the most creative mathematicians ever, and surely the greatest mathematician of the Constructivist ("intuitionist") style. Poincaré is sometimes called the Father of Topology (a title also used for Euler and Brouwer), but produced a large amount of brilliant work in many other areas of mathematics, and also found time to become a famous popular writer of philosophy, saying, for example, "Mathematics is the art of giving the same name to different things."

Poincaré's achievements include combinatorial (or algebraic) topology, the theory of differential equations, foundations of homology, the theory of periodic orbits, and the discovery of automorphic functions (a unifying foundation for the trigonometric and elliptic functions) 

Principle of relativity and Lorentz transformations

He discussed the "principle of relative motion" in two papers in 1900 and named it the principle of relativity in 1904, according to which no physical experiment can discriminate between a state of uniform motion and a state of rest. In 1905 Poincaré wrote to Lorentz about Lorentz's paper of 1904, which Poincaré described as a "paper of supreme importance." In this letter he pointed out an error Lorentz had made when he had applied his transformation to one of Maxwell's equations, that for charge-occupied space, and also questioned the time dilation factor given by Lorentz. In a second letter to Lorentz, Poincaré gave his own reason why Lorentz's time dilation factor was indeed correct after all: it was necessary to make the Lorentz transformation form a group and gave what is now known as the relativistic velocity-addition law. Poincaré later delivered a paper at the meeting of the Academy of Sciences in Paris on 5 June 1905 in which these issues were addressed. In the published version of that he wrote:

 The essential point, established by Lorentz, is that the equations of the electromagnetic field are not altered by a certain transformation (which I will call by the name of Lorentz) of the form:

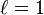and showed that the arbitrary function must be unity for all (Lorentz had set by a different argument) to make the transformations form a group. In an enlarged version of the paper that appeared in 1906 Poincaré pointed out that the combination x² + y² + z² − c²t² is invariant. He noted that a Lorentz transformation is merely a rotation in four-dimensional space about the origin by introducing 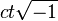as a fourth imaginary coordinate, and he used an early form of four-vectors. Poincaré’s attempt at a four-dimensional reformulation of the new mechanics was rejected by himself in 1907, because in his opinion the translation of physics into the language of four-dimensional geometry would entail too much effort for limited profit. So it was Hermann Minkowski who worked out the consequences of this notion in 1907.

Awards :

    * Oscar II, King of Sweden's mathematical competition (1887)

    * American Philosophical Society 1899

    * Gold Medal of the Royal Astronomical Society of London (1900)

    * Bolyai Prize in 1905

    * Matteucci Medal 1905

    * French Academy of Sciences 1906

    * Académie Française 1909

    * Bruce Medal (1911)

Named after him :

    * Poincaré Prize (Mathematical Physics International Prize)

    * Annales Henri Poincaré (Scientific Journal)

    * Poincaré Seminar (nicknamed "Bourbaphy")

    * The crater Poincaré on the Moon

    * Asteroid 2021 Poincaré