Relation between the integer numbers set and rational numbers set
We know that I = {.........................,-5,-4,-3,-2,-1, 0, 1, 2, 3, 4, 5, ............................ }
We know that I = {.........................,-5,-4,-3,-2,-1, 0, 1, 2, 3, 4, 5, ............................ }
Q= {X :X= p/q and p,q ∈ I and q ≠ zero }
then we can say that every integer number is also rational number his denominator = 1 then we can
I = {.........................,-5/1,-4/1,-3/1,-2/1,-1/1, 0/1, 1/1, 2/1, 3/1, 4/1, 5/1, ............................ }
but not every rational number is also integer number but in one case if the numerator is divisible by the denominator for instance 12 /4 is rational number and also integer number because 12 /4 = 3 and also 15/5=3 , 20/4= 5, 90/3 = 30 and 21/7 = 3
-----------------------------------------------------------
Various forms of the rational number :
the value of any rational number is not changed if we multiply or divide denominator and numerator by one number not equal zero
ex : find two numbers equal 3/2
decimal form for rational number
write 8/12 in the simplest form
SOLVED PROBLEMS
to write the rational number in the decimal form we should make the denominator Multiples of 10 by use Previous property
ex : write 5/2 in the decimal form.
ex2: write 6/8 and 1/6 in decimal form.
Percentage form for rational number
to write the rational number in the percentage form we should make the denominator 100 only
ex : write 5/20 , 5/16 and 5 (12/125) in Percentage form
Simplest form for rational number
to write the rational number in the simplest form we should divide denominator and numerator by highest common factor (hcf)
write 8/12 in the simplest form
SOLVED PROBLEMS
find X to make 75/X and 15/(X+1)
75/X is natural number if X = { 1, 3, 5, 15, 25, 75} because 75 is divisible by { 1, 3, 5, 15, 25, 75}only
15/ (X+1) is integer number if X = {0 ,2 ,4 ,14}because 15 is divisible by {1,2,5,15}only
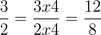







ليست هناك تعليقات:
إرسال تعليق